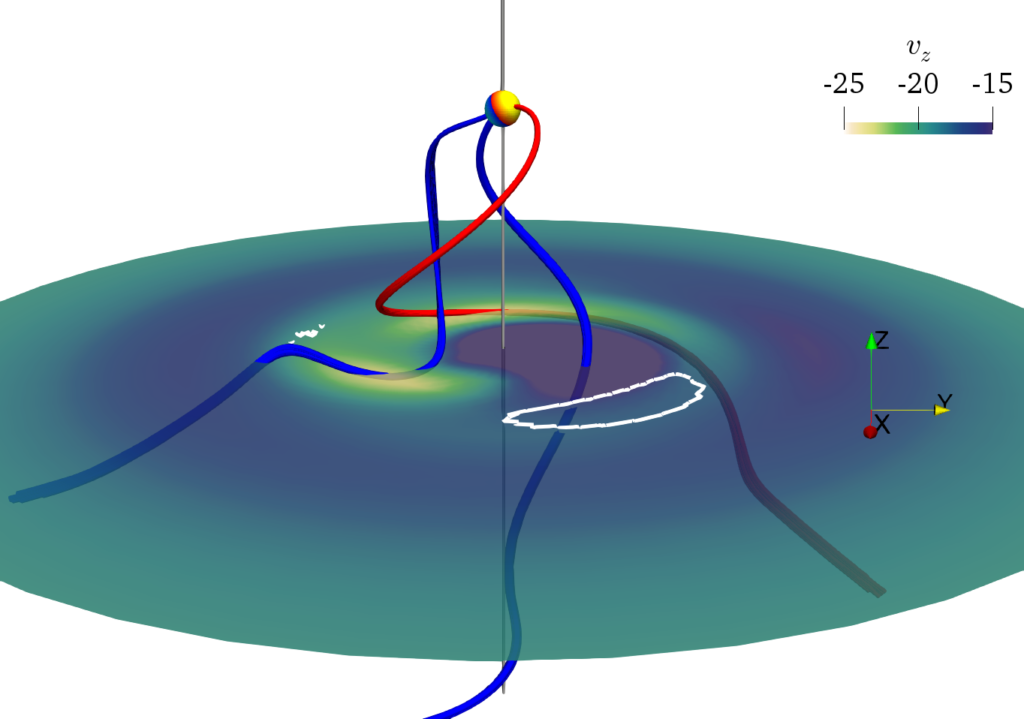
Abstract: We present magnetohydrodynamic simulations of a fast-rotating planetary magnetosphere reminiscent of the planet Uranus at solstice, that is, with the spin axis pointing to the Sun. We impose a 10 times faster rotation than for Uranus, in order to emphasize the effects of rotation on the magnetospheric tail without the need of an excessively large simulation domain while keeping the qualitative aspects of a supersonic magnetized solar wind interacting with a fast-rotating magnetosphere. We find that a complex helical Alfvénic structure propagates downstream at a velocity exceeding the plasma velocity in the magnetosheath. Similarly, the reconnection regions, which mediate the interaction of the planetary magnetic field and the interplanetary magnetic field, do also form a helical structure with the same downstream velocity but a 2 times larger pitch. We speculate that the magnetic field of the helical structure connected to the interplanetary magnetic field asymptotically reduces the phase velocity of the helical structure toward the tailward velocity in the magnetosheath. For our simulations we use the MPI-AMRVAC code which we enhanced with a time-dependent background magnetic field in the splitting of the magnetic field.

©2018. American Geophysical Union. All Rights Reserved.

Rarefaction and compressional standing slow mode structures in Mercury’s magnetosheath: 3D MHD simulations

Authors: Pantellini, Filippo; Griton, Léa; Varela, Jacobo
Publication: Planetary and Space Science, Volume 112, p. 1-9. (P&SS Homepage)

Keywords: MHD simulations, Mercury, Magnetosphere, Slow mode waves
Abstract Copyright: (c) 2015 Elsevier Ltd
DOI: 10.1016/j.pss.2015.04.007

Abstract
We show that slow mode compressional fronts form upstream of the day side magnetopause in MHD simulations of Mercury’s magnetosphere. The strongest compressional fronts are located upstream of the magnetopause with strong magnetic shear. Compressional fronts are crossed by magnetic field lines connecting the interplanetary magnetic field and the planet’s intrinsic field, their role is to bend the magnetic field in the magnetosheath towards the magnetopause. Besides these compressional fronts, already observed in space and theoretically discussed by various authors for the case of the Earth, we observe the formation of a slow mode standing rarefaction wave spatially growing over a substantial fraction of the distance between the bow shock and the magnetopause. The slow mode source region for the rarefaction waves is located in the magnetosheath, near the bow shock’s nose. The generated standing rarefaction waves, however, form even at large distances from the source region along the magnetospheric flanks. They fine-tune the magnetic field line draping and plasma flow around the magnetopause. In ideal MHD the magnetospheres of Mercury, the Earth and the giant planets do closely resemble each other, we therefore expect the mentioned slow mode structures not to be specific to Mercury.

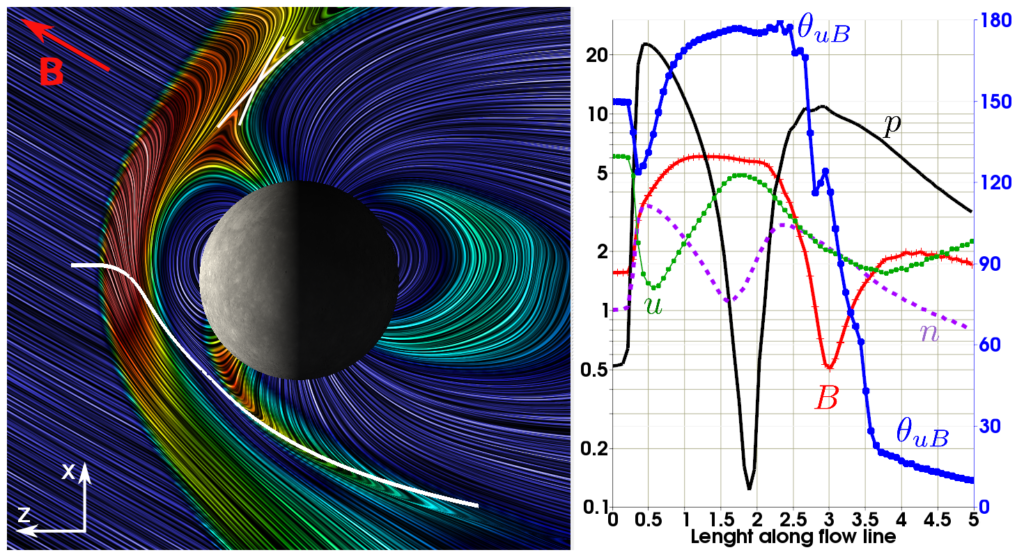See the paper for the legend of this figure.  (c) 2015 Elsevier Ltd

Identification of standing fronts in steady state fluid flows: exact and approximate solutions for propagating MHD modes

Authors: F. Pantellini and L. Griton

DOI: 10.1007/s10509-016-2921-y

Journal: Astrophysics and Space Science, Volume 361, Issue 10, article id.335, 11 pp.

Abstract:

The spatial structure of a steady state plasma flow is shaped by the standing modes with local phase velocity exactly opposite to the flow velocity. The general procedure of finding the wave vectors of all possible standing MHD modes in any given point of a stationary flow requires numerically solving an algebraic equation. We present the graphical procedure (already mentioned by some authors in the 1960’s) along with the exact solution for the Alfvén mode and approximate analytic solutions for both fast and slow modes. The technique can be used to identify MHD modes in space and laboratory plasmas as well as in numerical simulations.

See the paper for the figure’s legend.